Лекция 4. Истоки классической логики: Парменид и Зенон Элейский

Пустовит А. В.

Нече выть, ты вечен.

Д. Авалиани

Итак, от чего же зависит правильность рассуждения (вернее сказать, истинность вывода)? Во-первых, от истинности посылок. Во-вторых, форма правильного рассуждения должна представлять собой один из законов логики. Только при соблюдении обоих условий можно быть уверенным в правильности (истинности) заключения (вывода).

Фактически все три закона Аристотелевой логики сводятся к запрету противоречия. – Почему это так? – Потому, что из противоречивого высказывания логически следует любое высказывание (если верно противоречие, то верно все что угодно). Если А и не-А, то В [Ивин А. А. Логика. – М., 2004, с. 161].

Правильно построенное рассуждение должно быть непротиворечивым (свободным от противоречий).

Проиллюстрируем этот логический закон простейшим математическим построением. То, что наличие противоречия губит содержательную научную теорию, можно показать следующим образом. Представим себе, что наряду с тривиальными равенствами 1=1, 2=2 и т. д., мы включили в систему верных (истинных) арифметических высказываний утверждение 1=2. Тем самым теория стала противоречивой, поскольку мы утверждаем 1=1, 2=2 (А=А, закон тождества) и одновременно 1=2 (А=В; но В не есть А, следовательно, А одновременно равно себе и не равно себе (равно другому).

А есть А (1=1) и в то же время А есть В (1=2) – это и есть противоречие.

Поскольку к обеим частям верного равенства можно прибавлять одно и то же число (если a = b, то a + 1 = b + 1) то из равенства 1=2, прибавив к левой и к правой части по единице, получим 2=3, еще раз прибавив по единице, получим 3=4 и т. д.; таким образом, придем к выводу: 1=2=3=4=…, т. е. любое натуральное число равно любому другому натуральному числу. Понятно, что при этом все арифметические доказательства рухнут; арифметика как содержательная теория перестанет существовать.

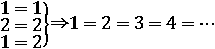
В противоречивой теории утрачивается различие между истиной и ложью [Бирюков Б. В. Жар холодных числ и пафос бесстрастной логики (Формализация мышления от античных времен до эпохи кибернетики). – М., 1985, с.119 – 120]), доказуемым становится все, что угодно. Такая теория не имеет никакой ценности. Следовательно, классическая логика имеет все основания для того, чтобы настаивать на запрете противоречия.

Однако, запрещая противоречие, Аристотель обездвиживает умопостигаемый мир. Почему это так? Потому что осмысление движения связано с противоречием. Задолго до Аристотеля на это указал великий древнегреческий философ Зенон Элейский, сформулировав свои знаменитые апории [Греческое слово «апория» означает «непроходимость, безвыходное положение» (Чанышев А. Н. Курс лекций по древней философии. – М., 1981, стр. 155)], – рассуждения о непостижимости, немыслимости движения.

Одна из апорий Зенона выглядит таким образом. Представим себе, говорит он, бегуна, который бежит по прямой от пункта А до пункта В. Расстояние от А до В равно 1. Как скоро он прибежит в В? – Любой человек, отвечая на этот вопрос, скажет: «Это зависит от скорости. Чем быстрее движется бегун, тем меньше времени понадобится ему для того, чтобы достичь пункта В».

Ответ Зенона озадачивает своей парадоксальностью: он утверждает, что бегун никогда не достигнет В. Вот доказательство: прежде, чем пробежать все расстояние от А до В, бегун должен преодолеть его половину (1/2). Пробежав половину пути, бегун, прежде чем оказаться в В, должен будет преодолеть половину оставшегося расстояния (1/4), то есть оказаться в точке, отстоящей от пункта А на расстоянии, равном 3/4 всего пути. После этого, прежде чем попасть в В, он снова должен будет сначала пробежать половину оставшегося расстояния (1/8), то есть дойти до «промежуточного финиша» в точке 7/8 и т.д. Иными словами, бегун должен пробежать расстояние, равное сумме ряда

1/2 + 1/4 + 1/8 + 1/16 + ………

Многоточие означает, что ряд продолжается до бесконечности. Каким образом, спрашивает Зенон, бегун может преодолеть бесконечную последовательность отрезков за конечное время? Ведь, сколько бы членов ряда мы ни взяли, достичь «конца пути» – нам так и не удастся, ибо не будет доставать отрезка пути, равного последнему взятому члену [Гарднер М. Математические новеллы. – М., 1974, с. 7-8].

Перед нами рассуждение, ни в чем не нарушающее законов логики, – и, однако, приводящее к нелепому выводу. Всем ведь прекрасно известно, что преодолеть конечное расстояние за конечное время можно. Легенда говорит о том, что первым критиком Зенона был его слушатель, киник Антисфен, который, не говоря ни слова, встал и прошел несколько шагов.

Движенья нет, сказал мудрец брадатый.

Другой смолчал и стал пред ним ходить.

Сильнее бы не мог он возразить;

Хвалили все ответ замысловатый.

Но, господа, забавный случай сей

Другой пример на память мне приводит:

Ведь каждый день пред нами солнце ходит,

Однако ж прав упрямый Галилей.

[Пушкин А. С. Собрание сочинений в десяти томах. – М., 1974 – 1978. Т.2, с.67].

– так излагает эту историю А. С. Пушкин в стихотворении «Движение». Зенон пояснил, что он доказывает вовсе не то, что движения нет, а лишь то, что оно немыслимо [Чанышев А. Н. Курс лекций по древней философии. – М., 1981, стр. 157].

Нелепо отрицать движение как очевидность, как чувственную достоверность, но (ведь чувства часто обманывают нас!) можно и должно поставить вопрос о его истинности. Как возможно (и возможно ли вообще) выразить движение в логике понятий?

Не является ли движение иллюзорным?

Дело в том, что иногда истина находится в резком противоречии с очевидностью (т. е. с тем, что видно глазами): например, смена дня и ночи обусловлена не движением Солнца вокруг неподвижной Земли (хотя люди веками верили в это), а вращением Земли вокруг своей оси. Итак, глаза ума (умо-зрение; по-гречески – теория, слово, однокоренное со словом «театр» – «зрелище» [Гаспаров М. Л. Занимательная Греция. Рассказы о древнегреческой культуре.- М., с. 370] видят совсем не то же самое, что просто глаза.

Еще один пример противоречия между истиной (сущностью) и очевидностью (видимостью), – знаменитая атомистическая гипотеза Демокрита, так блестяще подтвержденная современной наукой. Демокрит утверждает, что краски, формы, запахи, вкусы – все это иллюзии. Не существует ни красного, ни синего, ни твердого, ни мягкого, ни горького, ни сладкого – все это только результаты взаимодействия человека с окружающим его миром, все это существует только в человеческом восприятии. Поистине же существуют только атомы и пустота.

Учитель Зенона, философ Парменид, настаивал на том, что движение – это иллюзия. Отрицая истинность движения, он утверждает неподвижность (неизменность) умопостигаемой истины. Цель апорий Зенона состояла в защите учения Парменида и его концепции неподвижной, неизменной истины. Зенон разбирал тезисы противников Парменида (например, что сущее множественно, что движение реально существует) и показывал, что все эти тезисы приводят к логическим противоречиям.

Главное сочинение Парменида – поэма «О природе». В центре внимания философа находятся две проблемы – вопрос об отношении бытия и небытия и вопрос об отношении бытия и мышления. Парменид утверждает: бытие есть, а небытия нет. А – бытие, не-А – небытие, – ведь не-бытие есть отрицание бытия. Утверждать, что бытие есть и, одновременно, что не-бытие тоже есть, означает допустить противоречие. Итак, ЕСЛИ бытие есть, ТО небытия нет.

Из того, что небытие не существует, Парменид делает безупречно логичный вывод о том, что бытие едино и неподвижно. В самом деле, разделить бытие на части могло бы лишь небытие, но его нет. Всякое изменение предполагает, что нечто исчезает и что-то появляется, но на уровне бытия нечто может исчезнуть лишь в небытии и появиться лишь из небытия, а небытия нет. Поэтому бытие и едино и неизменно [Чанышев А. Н. Курс лекций по древней философии. – М., 1981, с.150-153]. Следовательно, истина о бытии тоже едина и неизменна (неподвижна).

Итак, Парменид утверждает: бытие есть, а небытия нет.Тем самым он, – задолго до Аристотеля, – неявно формулирует один из законов логики – закон противоречия (непротиворечивости): ложно, что А и не-А.

Зенон защищает учение Парменида, доказывая, что попытка осмыслить движение приводит к логическому противоречию. Мышление и бытие тождественны; бытие едино и неподвижно, значит, и мышление должно быть таким же, единым и неподвижным, т. е. непротиворечивым. Если, пытаясь мыслить движение, мы впадаем в противоречие, значит, движение не существует:

«…именно у Парменида мы впервые находим формулировку принципа исключенного третьего, а доказательства Зенона Элейского путем приведения к абсурду знамениты и сейчас» [Бурбаки Н. Очерки по истории математики. – М., 1963, с.11].

Философской системе Парменида и Зенона противостоят идеи другого великого греческого философа, современника Парменида, Гераклита Эфесского. Учение Гераклита строится на двух неразрывно связанных друг с другом философских идеях, – это единство противоположностей (противоречие) и движение.

Первая и притом важнейшая идея Гераклита – это идея борьбы и единства (тождества) противоположностей.

«Сопряжения: целое и нецелое, сходящееся расходящееся, созвучное несозвучное, из всего – одно, из одного – все» [Фрагменты ранних греческих философов. Часть 1. От эпических теокосмогоний до возникновения атомистики. Издание подготовил А. В. Лебедев. – М., 1989, с. 198-199].

«Путь вверх-вниз один и тот же» (с.204). «Одно и то же в нас – живое и мертвое, бодрствующее и спящее, молодое и старое, ибо эти [противоположности], переменившись, суть те, а те, вновь переменившись, суть эти” (с. 213-214).

«Бессмертные смертны, смертные бессмертны, [одни] живут за счет смерти других, за счет жизни других умирают”.(с.215)

“Они не понимают, как враждебное находится в согласии с собой: перевернутое соединение (гармония), как лука и лиры”. (с.199).

“Из различающегося прекраснейшая гармония “ (с.21).

“Одно-единственное Мудрое [Существо] называться не желает и желает именем Зевса” (с.239).

Итак, все в мире состоит из противоположностей, противоборствующих сил и тенденций. Действуя одновременно, эти противоположно направленные силы образуют напряженное состояние, которым и определяется внутренняя гармония вещей. Эту мысль Гераклит поясняет знаменитым примером лука и лиры. Оба конца лука стремятся разогнуться, но тетива стягивает их, и эта взаимная сопряженность образует высшее единство.

Вторая важнейшая идея Гераклита – это идея безостановочной изменчивости вещей, их текучести.

“Нельзя войти в одну и ту же реку дважды и нельзя тронуть дважды нечто смертное в том же состоянии, но, по причине неудержимости и быстроты изменения, все рассеивается и собирается,, приходит и уходит… Мы входим и не входим в одну и ту же реку, мы те же самые и не те же самые” [Реале Дж., Антисери Д. Западная философия от истоков до наших дней. Т.1. Античность. СПб., 1994, с.24].

Эта сторона учения Гераклита стала особенно популярной у его последователей (например, у Кратила), и в сознание последующих поколений Гераклит вошел прежде всего как философ, учивший, что “все течет”. Это выражение не фигурирует ни в одном из дошедших до нас фрагментов Гераклита, однако мы находим его при изложении взглядов Гераклита у Платона (Теэтет, 182С, Кратил 440) и у Аристотеля (Метафизика, XIII 4. 1078b 13) [Рожанский И.Д. Ранняя греческая философия. – в кн.: Фрагменты ранних греческих философов. Часть 1. От эпических теокосмогоний до возникновения атомистики. Издание подготовил А. В. Лебедев. – М., 1989, с.20-21].

Ясно, что воззрения Гераклита противоположны воззрениям Парменида. Отвергая возможность и мыслимость небытия, Парменид мимоходом обрушивается на «двухголовых» людей, «у кого «быть» и «не быть» считаются одним и тем же и не одним и тем же и для всего имеется обратный путь». Этот полемический выпад, несомненно, направлен против Гераклита и его последователей.

Итак, Гераклит учит о тождестве противоположностей и о вечной изменчивости всего сущего (“все течет”). Эти две идеи связаны между собой: попытка осмыслить движение приводит к логическому противоречию; как впоследствии сформулирует великий последователь Гераклита, Гегель, «движение есть само существующее противоречие». Именно учение Гераклита стало основой диалектической логики Гегеля, писавшего о том, что нет ни одного положения Гераклита, которое он (Гегель) не взял в свою логику [Гегель Г. В. Д. Сочинения. М.; Л., 1932, т. 9, с.246].

Итак, у самых истоков европейской культуры мы видим противостояние двух диаметрально противоположных точек зрения.

Вся последующая история европейской мысли может быть описана как противостояние линии Парменида и линии Гераклита, закона исключенного третьего и принципа совпадения противоположностей, концепции неподвижной истины и представления об истине как о процессе (движении, изменении, развитии).

Первая концепция состоит в том, что бытие есть, а небытия нет, истина едина и неподвижна, а мышление должно быть непротиворечивым. Вторая настаивает на том, что существует не только бытие, но и небытие. Объединение (синтез) этих двух категорий, – бытия и небытия, – приводит к категории становления:

«Становление содержит в себе бытие и ничто и содержит их таким образом, что оба они полностью переходят друг в друга… Становление, таким образом, оказывается безудержным движением…» [Гегель Г. В. Ф. Энциклопедия философских наук. Наука логики. Т.1. – М., 1974, с.228].

Гегель отзывается о Гераклите с восторгом:

«Что касается общего принципа, то мы должны сказать, что этот смелый ум …первым молвил глубокое слово: «Бытие и небытие тождественны, все и есть и не есть одновременно». Истинное существует лишь как единство безусловных противоположностей, а именно как единство чистой противоположности бытия и небытия… Но мы имеем еще одно высказывание, которое точнее указывает смысл этого принципа… Гераклит утверждает: «Все течет, ничто не бывает и не остается неизменным»… Ближайшим определением для этого общего принципа является становление, истина бытия; поскольку все есть и одновременно не есть, то Гераклит этим выразил, что мир есть становление. В последнее входит не только возникновение, но и исчезновение; оба они не самостоятельны, а тождественны. Такова эта великая мысль – перейти от бытия к становлению» [Гегель Г. В. Ф. Лекции по истории философии. Книга первая. – СПб., 1993, с. 290].

Следуя Гераклиту Гегель утверждает: «Истина есть процесс».

Итак, что есть сущее ? является ли оно неподвижным или изменчивым? является ли оно бытием или становлением? Вот как отвечает на этот вопрос выдающийся ученый ХХ в., создатель синергетики И. Пригожин: «Мы считаем, что бытие и становление должны рассматриваться не как противоположности, противоречащие друг другу, а как два соотнесенных аспекта реальности» (Пригожин И. Порядок из хаоса, с.273).

Существует ли движение? – один из вечных вопросов философии, на который возможны два противоположных ответа.

Вопрос о реальности движения и о возможности его мыслить (или, в другой формулировке, вопрос о противоречивости или непротиворечивости истины) пройдет красной нитью через всю историю европейской философии (вспомним о том, что великий философ ХХ века Мартин Хайдеггер (1889-1976) определил сущность философии как вопрошание; философия – наука не ответов, но вопросов) и доживет до нашего времени [см. например: Яновская С. А. Преодолены ли в современной науке трудности, известные под названием “апорий Зенона”? – Яновская С. А. Методологические проблемы науки. М., 1972].

Создатель логики Аристотель избирает линию Парменида. Он сам пишет об этом в „Метафизике” очень ясно:

„…в поиски за истинным необходимо отправляться от того, что всегда находится в том же самом состоянии и не подвергается никакому изменению” [цит. по: Розенталь М. М. Принципы диалектической логики. – М., 1960, с. 100].

Аристотелевская логика, запрещающая противоречие, изгоняет движение из области науки.

Все три закона классической логики взаимосвязаны: они порождают особый мир – неподвижный мир без времени, без изменений, мир самотождественных неизменных объектов (примером такого мира может служить арифметика, в основе которой – натуральный ряд 1, 2, 3…; натуральные числа как раз и представляют собою самотождественные неизменные объекты). Законы арифметики суть вечные истины. Другим примером является геометрия – точки, прямые, плоскости тоже являются объектами такого рода. Евклид пишет о том. что математические предметы чужды движению.

Впрочем, о неподвижной истине пишет еще учитель Аристотеля, Платон, в диалоге „Кратил”. Если, рассуждает он, предмет, который мы изучаем, не изменяется, если он неизменен и неподвижен, то и знание о нем не должно изменяться. То, что было истинным, так и остается истинным, а то, что было ложным – остается ложным. В этом случае знание надежно и истинно.

Если же предмет изменяется, то и знание должно измениться; то, что было истинным, может стать ложным, а то, что было ложным, может стать истинным. Следовательно, заключает Платон, в изменчивом (подвижном) знания не бывает; там, где всегда происходит изменяемость, не может быть знания [«там по справедливости нельзя указать и на знание… где все вещи изменяются и ничто не стоит. Ведь если это самое знание есть знание того, что не изменяется, то знание всегда пребывает и всегда есть знание: а когда изменяется и самый вид знания, то как скоро вид знания изменяется в иной, знания уже нет, и где всегда происходит изменяемость, там никогда не бывает знания…» (Платон. Сочинения. В 3 т. – М., 1968 – 1972. Т.1, с. 440)].