Приложение 2. Обобщенная модель деятельности менеджера в системе управления
Бритченко И.Г., Бритченко Г.И.
Сложность анализа поведения руководителя связана с высокой неопределенностью математического описания их имитационных моделей. Один из возможных подходов к преодолению указанных препятствий состоит в выборе наиболее эффективных решений в зависимости от вида и степени информационной неопределенности. Процесс выбора эффективного решения включает обоснование критериев, позволяющих сформулировать количественные оценки эффективности. Последняя заключается в выборе компромиссного решения, невозможном без обоснования принципа компромисса.
Задача выбора оптимальных стратегий руководителя в многокритериальной ситуации заключается в ранжировании возможных решений по множеству частных (локальных) критериев. В качестве первого этапа решения этой задачи может быть выбор множества частных критериев, интегрально отображающих рассматриваемую деятельность руководителя.
1. Модель целевого блока. Введем обозначения:
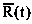– обобщенная количественная оценка набора показателей полезности деятельности руководителя (Q1, Q2, … Qn);
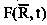– обобщенная количественная оценка набора показателей ресурсоемкости руководителя;
Δt = tк – tн – плановый период дискретного управления системой (tн – начало, tк – конец);
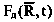– обобщенная стратегия поведения руководителя;
– допустимая стратегия, обеспечивающая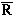 
при фиксированных значениях .
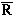Тогда формализованная цель деятельности руководителя будет иметь вид:
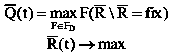
II. Модель коммуникативного блока. Условные обозначения:
Q – множество коммуникативных единиц (совещания, беседы, консультации и т.п.);
τ – время запаздывания, обусловленное отсутствием у руководителя информации об изменениях;
Ψ – индивидуальный оператор информационного отображения деятельности руководителя;
I – множество характеристик, отображающих коммуникативное множество у руководителя;
П – индивидуальный оператор пассивного поведения руководителя;
П’ – индивидуальный оператор пассивного поведения руководителя;
I(t) = ψ[Q(t – τ), t]
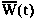– обобщенная характеристика активного поведения руководителя;
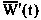– обобщенная характеристика пассивного поведения руководителя;
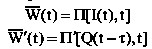
Формализованная модель коммуникативной деятельности разработки будет иметь вид:
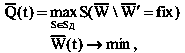
где SД – допустимая стратегия деятельности руководителя.
III. Модель выработки решения. Условные обозначения:
Х – допустимое множество решений;
х – определенное на множестве Х решение;
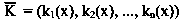– вектор частных критериев.
OptG – обобщенный критерий оценки эффективности принимаемого руководителем решения.
Выбор оптимального решения в многокритериальной ситуации опишется соотношением:
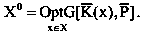
Исходя из аналитико-эвристического подхода, можно наметить следующие этапы решения проблемы выбора решений:
1. Формирование функций полезности частных критериев;
2. Формирование обобщенного критерия оценки эффективности и оптимизации.
1. Формирование функций полезности локального критерия запишем следующим образом (Теория выбора и принятия решений / Макаров И.М., Виноградская Т.М. и др. – М.: Наука, 1988. – 382 с.):
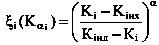
где Ki – текущее значение i-го частного критерия;
Кінх – его наихудшее значение; соответствует границам приближенной области компромисса
Кінл – его наилучшее значение;
αi – показатель нелинейности
При 0 < αi < 1 – кривая выпуклая, αi > 1 – кривая вогнутая; αi = 1 – линейная независимость.
При определении приближенной области компромиссов (Кінл, Кінх) положим, что на множестве допустимых решений Х проводится оптимизация по каждому из частных критериев Ki:
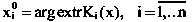
Тогда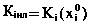 
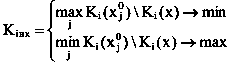
2. Формирование обобщенного критерия оценки эффективности и оптимизации выработки решений. Чтобы выбрать единственное решение из области компромиссов, необходимо обосновать аксиоматику и на этой основе сформулировать правило принятия решения (схему компромисса) в условиях многокритериальности.
Введем условные обозначения:
а1 – количественная характеристика весовых коэффициентов частных критериев К(х);
ξi(Кi) – функции полезности честных критериев Кi;
х0 – оптимальное решение;
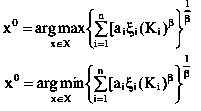
β – коэффициент жесткости принимаемого решения.
Предположим, коэффициенты аi заданы количественно, но не точно, а в виде интервала (ai min, ai max), причем иногда на интервале известны некоторые предпочтения в виде плотности вероятностей, функции принадлежности некоторому неопределенному множеству. Используем двухуровневую процедуру выбора компромиссного решения. На первом этапе определяется подобласть допустимых решений в пространстве частных критериев K = {Ki}, i = 1,… n ограниченная значениями Ki, которые соответствуют вариациями (аі.
Для этого решаем n задач оптимизации вида:
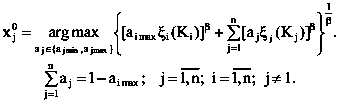
Значения β выбираются в зависимости от информации о выпуклости оптимизируемой функции. По значениям xi0, i = 1… n вычисляем
т.е. устанавливаем границы области, из которой на втором этапе находится компромиссное решение. На втором этапе согласно выражению
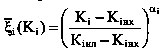
формируем функции полезности и по минимальной схеме
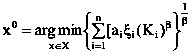
находим компромиссное решение. Значение параметра αi определяется эвристически на основе информации о предпочтениях на интервале изменения аi (если они не заданы αi = 1).
IV. Модель реализационного блока. Эту модель можно трактовать как задачу перевода объекта из некоторого начального состояния Х0 в заданное или желаемое Хк (конечное). Траектория такого перехода в фазовом пространстве определяется оператором функционирования Ф, устанавливающим связь текущего объекта Х(t) с управляющим воздействием U(t), возмущениями η(t) и начальным состоянием Х0, т.е.
X(t) = Ф[Х0, t0, U(t0, t), η(t0, t)]
Важное значение имеет задача выбора оператора формирования П
U(t) = П[x(t), Xk, t]
При этом должен экстремизироваться некоторый выбор критериев эффективности
K = {K, (X, U)}, i = 1
учитывающих степень достижения желаемого состояния Х и эффективность собственно управляющего воздействия U.
Управляющее воздействие U можно представить как
U[x(t), Xk, t] = U*(t) + U[x(t), X*(t), t]
где U*(t) – программное управляющее воздействие, соответствующее оптимальной траектории;
X*(t) – переход из начального (X0, t0) в заданное конечное (Xk, t0) состояние, а U[x(t), X*(t), t] – управление, компенсирующее отклонение от X*(t).
Общий критерий оценки реализации управления можно представить в виде:
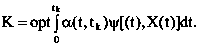
где tk – время управления;
φ – знакоопределенная функция, обуславливающая вид критерия оптимальности;
X(t), X*(t) – физическое и программное состояние объекта управления в момент времени t.
α(t, tk) – функция, определяющая характер взаимодействия системы с внешней средой.
В случае α(t, tk) = 1 – непрерывное взаимодействие.
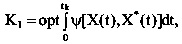
а при α – дискретном α(t, tk) = &delta(t – Tn).
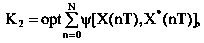
где Т – интервал дискретности.
Установим связь функции ψ = [X(t), X*(t)] с особенностями цели реализации решений. Пусть ψ – функция эффекта реализации, тогда необходимо ее максимизировать:
ψ = [X(t), X*(t)] = max[F(t) – L(t)]
где F(t) – эффект, полученный при отклонении от плановой траектории;
L(t) – затраты на реализацию решений.
Эффект F(t), получаемый при этом, определяется уравнением
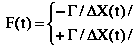
где – Г, + Г – матрицы строки затрат за отклонение от плана (решения) при его невыполнении и перевыполнении;
ΔХ(t) – матрица-столбец изохронных отклонений от плана. Матрица – Г во всех случаях неположительная, а + Г – неположительная при недопустимости перевыполнения плана и неотрицательная в противном случае; в общем случае (+Г) = (–Г).
В общем случае L(t) включает матрицу затрат Е(t), определяемых затратами управляющего воздействия, Z(t) – матрицу затрат на создание и поддержание в работоспособном состоянии ресурсов, необходимых для управления, т.е.
L(t) = Z(t) + Е(t),
где Z(t) – затраты всего планового периода Т = tk – tн; т.е.
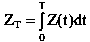
Здесь Z(t) – по сути затраты в единицу времени на создание и содержание в работоспособном состоянии системы управления. Эффект Fc вследствие отклонения от плана и затраты Еc на корректировку управления, необходимые для компенсации этого отклонения, пропорциональны только времени отклонения процесса от планового
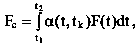
где F(t) – функция эффекта;
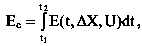
где E(t, ΔХ, U) – затраты на управляющие воздействия, является функцией времени, отклонения ΔХ и виды воздействия U;
t2 = tкн + tп.р. + tзап. + tп.п. – время ликвидации отклонения от плана;
tкн – время с момента возникновения отклонения от плана до ближайшего момента контроля процесса (при непрерывном контроле tкн = 0);
tп.р. – время, необходимое для анализа ситуации и принятия решения;
tзап. – время запаздывания, требуемое для изменений в системе, связанных с управлением;
tп.п. – время переходного процесса с момента начала управления до ликвидации отклонения.
Тогда функция эффекта системы при нежелательном отклонении от плана:
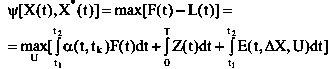
При желательном отклонении от плана:
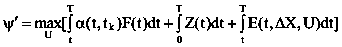
Представленная модель деятельности руководителя как система четырех крупно агрегированных подсистем – целевой, коммуникативной, оценочной и реализационной – является обобщенной. На ее базе могут быть разработаны конкретные методики оценки руководителей при принятии решений, использование которых будет полезным при выборе руководителей в условиях перестройки.