Види функціональної залежності та особливості індексного аналізу

Андрієнко В.Ю.

Об’єктом індексного аналізу є функціональна залежність між явищами. Її традиційне визначення в статистиці зводиться приблизно до наступного: функціональна залежність між явищами має місце тоді, коли одне явище, що іменується об’ємним показником, можна представити у вигляді добутку двох інших показників, один з яких є кількісним, другий – якісним. Класичний приклад такої залежності: загальна вартість певного товару (Q) дорівнює виробленій кількості даного продукту (q), помноженій на його ціну (р): Q = рq.

Приведене визначення, в принципі, вірне, але досить абстрактне. У ньому однозначно відображена лише математична сторона питання, але не розкритий його матеріальний зміст, тобто залишається поза увагою суть функціональної залежності в її причинно-наслідковому сенсі. Практика свідчить, що розгляд функціональної залежності тільки в математичному плані не може бути надійною основою індексного аналізу. Без визначення економічної суті функціональної залежності індексний аналіз з дійового статистичного методу пізнання може перетворитися в набір безплідних математичних вправ. Про небезпеку такого переродження свідчать чисельні приклади з практики багатофакторного індексного аналізу, який досить часто схожий на "гру в цифри". І це зрозуміло, адже при бажанні самі різнорідні і незалежні один від одного явища математично можна виразити у вигляді "функціональної" залежності між ними.

Математичним елементом відображення функціональної залежності між двома явищами виступає відносна величина, обчислена з співвідношення даних явищ. Наприклад, щоб сукупність А виразити функціонально залежною від сукупності Б, досить скласти рівняння: А = Б (А/Б). Але основне призначення індексного методу полягає не в складанні і розв’язанні подібних рівнянь, а в попередньому осмисленні питання про те, чи мають вони економічне значення і пізнавальну цінність. Важливість аналізу взаємозв’язків, по суті, полягає в тому, щоб за математичною формою відображення функціональної залежності бачити причинно-наслідковий зв’язок між явищами. Разом з тим такий зв’язок часто відсутній не тільки між незалежними, але і взаємопов’язаними явищами. Скажімо, такі сукупності, як чисельність населення N і наявність житлової площі S, пов’язані між собою самим безпосереднім чином, але функціональну залежність типу NS (N/S) не можна вважати реальною в причинно-наслідковому сенсі, оскільки чисельність населення безпосередньо не зумовлюється наявністю житлової площі.

Спробуємо здійснити певну класифікацію індексних взаємозв’язків відповідно до їх внутрішнього змісту, використавши в якості об’ємного показника кількість електроенергії (Е), що виробляється за рік. Виразимо його через залежність від наступних показників:

1. E = K(E/K);

2. E = R(E/R);

3. E = N(E/N);

4. E = X(E/X);

де К – кількість електростанцій, що діяли; R – кількість споживачів електроенергії; N – середньорічна чисельність населення; X – протяжність ліній електропередач.

Всі кількісні показники, що знаходяться в правій частині рівнянь, так чи інакше пов’язані з обсягом виробництва електроенергії, а тому моделі в математичному відношенні коректні. Але вони далеко не рівнозначні з точки зору причинно-наслідкової залежності.

Оскільки функціональна залежність має місце тоді, коли зміна величини одного явища слугує реальною передумовою зміни величини іншого, можна з упевненістю сказати, що цій умові відповідає лише рівняння 1. Дійсно, зміна кількості електроенергії безпосередньо залежить від зміни кількості електростанцій та їх середньорічної потужності, адже будівництво нових електростанцій саме і переслідує мету розширити виробництво електроенергії.

Друга модель, що відбиває залежність кількості електроенергії від кількості її споживачів, викликає суперечливе почуття: в якійсь мірі залежність здається реальною і в той же час нереальною. Невизначеність в оцінці даної залежності посилюється тим, що її можна трактувати і в зворотному напрямку, тобто як залежність зміни кількості споживачів електроенергії від зміни обсягу електроенергії, що виробляється. Іншими словами, причину і наслідок встановити однозначно тут не досить проблематично.

Третя модель, що відбиває залежність обсягу електроенергії від чисельності населення, виглядає зовсім надуманою, оскільки важко уявити, яким чином зміна чисельності населення в ту або іншу сторону може адекватно відбитися на кількості електроенергії, що виробляється.

Четверта модель, що відбиває залежність обсягу електроенергії від протяжності ліній електропередач, спотворена у напрямі, бо насправді реальною є зворотна залежність: протяжність ліній електропередач залежить від кількості електроенергії, що виробляється та середньої відстані передачі кожної одиниці електроенергії.

Розглянутий приклад свідчить: якщо навіть абстрагуватися від явно спотворених моделей функціональної залежності, можна виділити принаймні три її різновиди:

а) реальну в причинно-наслідковому сенсі (модель 1);

б) невизначену з точки зору однозначного розпізнавання причини і наслідку (модель 2);

в) такої, що не має економічного значення (модель 4).

Для їх розмежування введемо відповідно поняття:

а) однозначно детермінований;

б) обопільно детермінований;

в) недетермінований взаємозв’язок між явищами.

Головна ознака однозначно детермінованого взаємозв’язку це дійсне призначення кількісного показника, що знаходиться в правій частині рівняння, для утворення результативного (об’ємного) показника. Для кількісного чинника, що виступає тут причиною, характерним є те, що він у часі передує результативному показнику (наслідку). Наприклад, чисельність працюючих або обсяг виробничих фондів призначені для виробництва продукції і у часі передують утворенню даного результативного показника. Внаслідок зазначених обставин для однозначно детермінованого взаємозв’язку характерне те, що її математична форма відображення відповідає реальному процесу утворення об’ємного показника. Так, в першій моделі загальний обсяг електроенергії дійсно складає суму індивідуальних розмірів вироблюваної електроенергії всіх електростанцій. При цьому кількісний чинник являє собою деяку "сукупність, що творить", кожна одиниця якої володіє певною "силою, що творить" (якісним показником).

У обопільно детермінованих взаємозв’язках поняття "що створюється" і "що творить" не мають однозначної фіксації і відображають інше економічне значення. На відміну від причинно-наслідкової залежності в творчому її сенсі тут має місце неминуча обумовленість зміни розмірів одного явища у зв’язку із зміною розмірів іншого з метою підтримки між ними певної пропорційності. Наприклад, у зв’язку із збільшенням кількості робочих місць неминуче зростання чисельності зайнятих, або навпаки. Але заздалегідь встановити, що тут первинне, а що вторинне, неможливо.

Оскільки в обопільно детермінованих взаємозв’язках об’ємний показник пов’язаний з двома іншими показниками за допомогою добутку, то зміна величини одного із співмножників з математичної точки зору спричиняє відповідну зміну величини об’ємного показника. Так в моделі (4) кількість споживачів електроенергії формально можна розглядати як чинник зміни загального обсягу електроенергії. Але з економічної точки зору питання повинне ставитися інакше: чи призводить в кожному конкретному випадку відносна зміна кількості споживачів електроенергії до відповідної зміни її загального обсягу? Відповідь буде негативною, оскільки прямо пропорційної залежності між цими явищами не існує, хоч імовірність зміни одного з них у зв’язку із зміною іншого досить значна. Отже, математичний і економічний підходи тут дещо не співпадають.

Для полегшення розпізнавання однозначно і обопільно детермінованих функціональних залежностей можна використати прийом їх перевірки на предмет зворотності зв’язків. Відомо, що причина і наслідок, що розглядаються в даному конкретному відношенні, є неповоротними. У справедливості цього легко пересвідчитися, якщо, наприклад, в моделі (1) в якості наслідку прийняти показник кількості електростанцій К, а в якості причини – загальний обсяг електроенергії і побудувати відповідну модель: К = Е×(К/Е). Така модель є беззмістовною. Оскільки причина і наслідок знаходяться не на своїх місцях. А в обопільно детермінованих залежностях прямі та обернені моделі є математично коректними.

Наявність зворотності функціональної залежності вказує на те, що маємо справу не з причиною і наслідком, а з паралельно існуючими і певним чином взаємопов’язаними явищами. Не маючи прямого впливу одне на одного, вони, вірніше, зміна пропорцій між ними, можуть впливати на інші, залежні від них явища. Такі моделі залежності в рамках індексного методу можуть бути використані для перетвореного виразу одного чинника через інші чинники.

Скажімо, в деякій індексній моделі присутній чинник обсягу основних виробничих фондів F. Відомо, що паралельно з ним діє чинник чисельності працюючих Т. Звідси чинник F можна перетворити в адекватну йому форму за формулою F = Т (F/T), де якісний показник являє собою рівень фондоозброєності праці. Дійсно, чисельність працівників і рівень їх фондоозброєності еквівалентні обсягу виробничих фондів. Показник чисельності працівників можна також представити еквівалентним обсягу основних виробничих фондів: Т = F (T/F), де якісний показник, будучи зворотним показнику фондоозброєності праці, відображає рівень працезабезпеченості основних фондів. Шляхом подібної "підстановки" досягається розгалуження індексних моделей з метою розширення кола чинників результативного показника.

Необхідно звернути особливу увагу на моделі, що відображають недетерміновані взаємозв’язки, подібні моделі (3). Така модель не може бути використана за прямим призначенням, тобто як модель залежності об’єму електроенергії від зміни чисельності населення і питомого виробітку електроенергії на одну людину. Не може вона застосовуватися і для еквівалентного перетворення одного показника в два інших показники, оскільки явища, що тут розглядаються, досить віддалені один від одного і зв’язок між ними на рівні конкретного аналізу є неістотним. Отже, моделі, що відображають недетерміновані зв’язки, в індексному факторному аналізі використовуватися не повинні.

Все це переконує в тому, що будь-яка індексна модель має математичну і логіко-аналітичну інтерпретацію. З математичної точки зору модель являє собою рівняння, яке дозволяє для кожного явища знайти перетворену форму його виразу у вигляді добутку двох інших явищ. Оцінка ж цього рівняння з логіко-аналітичної точки зору дозволяє встановити, чи існує реальна причинно-наслідкова залежність між ними, чи ні. Якщо така залежність існує, значить, знайдена реальна форма функціональної залежності об’ємного показника від його кількісного і якісного чинників, і тому модель придатна для використання за прямим призначенням. У іншому випадку модель самостійного значення не має і може бути використана лише для деталізації одного фактора за допомогою двох інших чинників. В основі такого перетворення лежить принцип еквівалентності між кількісними рівнями явищ. Якщо виявиться, що модель відображає недетермінований взаємозв’язок між явищами, то внаслідок некоректності вона повинна бути замінена іншою моделлю.

Викладене дозволяє зробити висновок щодо наявності двох принципово різних видів середніх величин, що іменуються в індексному аналізі якісними чинниками. У першому випадку якісна ознака являє собою середню творчу можливість кожного члена однієї сукупності з метою утворення іншої сукупності, у другому – середній розмір однієї сукупності, що припадає на одиницю іншої. Наприклад, рівень продуктивності праці робітників відображає середню продукуючу здатність кожного робітника, а рівень фондоозброєності праці робітників – середній розмір основних фондів, що припадає на одного робітника. Аналогічно можна обчислити багато інших показників, що відображають середній розмір одного явища в розрахунку на одного робітника (наприклад, середній рівень електроозброєності праці, середній розмір виробничої площі, що припадає на одного робітника тощо). В той же час середня можливість одного робітника може бути відображена тільки одним якісним показником – рівнем продуктивності праці.

Отже, є підстави для того, щоб якісні показники, що обчислюються по відношенню до однієї і тієї ж сукупності, поділяти на дві групи: внутрішні (ендогенні) і зовнішні (екзогенні). Перші мають місце в умовах однозначно детермінованого, а другі – обопільно детермінованого взаємозв’язку між явищами. Скажімо, середня врожайність – ендогенний показник посівних площ, а середня величина насиченості поголів’я худоби у розрахунку на гектар посіву – екзогенний показник по відношенню до посівних площ. Між ендогенними і екзогенними показниками однієї і тієї ж сукупності існує кількісна відмінність. Вона полягає в тому, що будь-яка сукупність має обмежену кількість ендогенних показників (частіше за все один), а коло екзогенних показників може бути безмежним. Так, творча здатність посівних площ характеризується одним показником – середньою врожайністю, в той же час по відношенню до посівних площ можна обчислити велику кількість екзогенних показників шляхом співвідношення їх з іншими явищами – наявністю технічних засобів обробки землі, добрив, що застосовуються тощо.

Між ендогенними і екзогенними показниками існують відмінності і схожість. За ознакою відмінності вони розчленовуються на дві неоднорідні групи, і ця їх властивість буде використана надалі для розв’язання одних проблем, а за ознакою схожості, що дозволяє об’єднувати їх у певні однорідні групи, – для з’ясування інших аспектів статистичного аналізу. Схожість між цими показниками виявляється на рівні формального, а відмінність – на рівні конкретного аналізу, про що йдеться нижче.

Таким чином, в рамках індексного аналізу за зовнішньою однотипністю якісних показників потрібно розрізняти їх сутнісну різнорідність, що дозволяє розчленовувати ці показники на ендогенні та екзогенні. Перші вказують на наявність причинно-наслідкової залежності між явищами (наприклад, між обсягом виробленої продукції і продуктивністю праці), другі являють собою своєрідний коефіцієнт взаємозв’язку між паралельно існуючими явищами, який слугує опосередкованою формою виразу одного явища через інше.

Виділені форми взаємозв’язків і відповідні їм види якісних показників не вичерпують проблему розподілу функціональних залежностей та особливостей індексного аналізу.

Мова йде про внутрішню сумірність або несумірність статистичних сукупностей, присутніх в індексних побудовах. Групу несумірних явищ складають, як правило, різнорідні продукти, динаміка яких визначається відомими індексами фізичного обсягу в поєднанні з індексами якісного показника-сумірника (ціни, собівартість тощо). Всі інші явища, що індексуються, є сумірними. Коло таких явищ досить широке. Загальним у них є те, що кількісні показники кожної окремої системи мають загальну одиницю вимірювання, завдяки чому вони стають сумірними, наприклад, посівні площі в індексах валових зборів сільськогосподарської продукції, чисельність працівників в індексах загального обсягу виробництва і т.д.

В умовах несумірних явищ існує лише одна форма побудови взаємопов’язаних індексних систем – так звана агрегатна форма. Так, агрегатний індекс загальних витрат на виробництво, що залежить від кількості вироблених товарів (q) та їх індивідуальної собівартості (z), має єдину форму відображення:

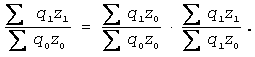
В умовах сумісних явищ можливі дві форми індексування. Скажімо, що той же індекс загальних витрат в умовах виробництва однорідної (сумірної) продукції q можна побудувати або аналогічно першому, або таким чином:

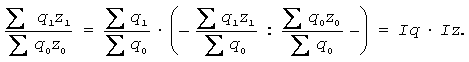
У цьому випадку має місце дезагрегована форма індексування кількісного і якісного чинників. Але головне не в формі, а в тому, що від форми індексування залежать результати впливу чинників на об’ємний показник, які (результати) нерідко арифметично не співпадають між собою. Ця обставина породжує проблему вибору з двох можливих прийомів індексування такого, який в більшій мірі відповідає вимогам факторного аналізу і забезпечує більш достовірні його результати. Іншими словами, існує відмінність в індексуванні сумірних і несумірних явищ, яка надалі знайде відображення в методології агрегатного індексування.

До істотної відмінності між сумірними і несумірними явищами належить також те, що для перших можливе обчислення усередненої якісної ознаки (середньої змінного складу), а для других такої можливості немає. Наприклад, для однорідної продукції обчислюється середня собівартість одиниці продукції, а для різнорідної продукції така середня неможлива і безглузда в принципі. Тому при сумірних явищах крім системи індексів кількісного і якісного чинників існує система індексів середньої змінного складу, що включає індекси фіксованого складу і структурних зрушень. Отже, індексування сумірних явищ має більш широкий діапазон і більш складну структуру, ніж індексування несумірних явищ, що в свою чергу породжує додаткові проблеми і особливості індексного аналізу.

Все це дозволяє зробити висновок про те, що в основі статистичного індексування лежить причинно-наслідкова залежність між явищами, і в цьому полягає його корінна відмінність від інших індексних побудов розрахункового але не аналітичного характеру. Останні використовуються як метод визначення необхідного показника на основі взаємопов’язаних з ним інших показників, але цей метод визначення нічого спільного не має з індексними моделями. Відомо, наприклад, що загальна кількість матеріалу т, необхідна для забезпечення необхідного випуску виробу q, визначається за формулою т = q × (m/q), де m/q середня витрата матеріалу на один виріб. Однак, з цього не випливає, що вказана формула являє собою реальну модель залежності між названими явищами. В межах причинно-наслідкової залежності первинним явищем (причиною) виступає кількість матеріалу, що використовується (т), а вторинним (слідством) кількість виробів, що випускаються (q). Тому реальна індексна модель буде мати вигляд: q = т × (q/m), де q/m – кількість виробів, що випускаються з одиниці матеріалу. Саме так будуються всі індексні моделі, засновані на взаємозв’язку типу "результат – витрати".

Деякі статистики, визнаючи причинно-наслідкову природу статистичного індексування, все ж допускають можливість існування моделей, в яких результативним показником виступає причина, а чинником наслідок, називаючи це непрямим індексуванням. Але в непрямому індексуванні особливої необхідності не існує, оскільки будь-яке соціально-економічне явище має свої безпосередні чинники і, отже, існує можливість прямого індексування.

Опубліковано : Андрієнко В.Ю. Cтатистичні індекси в економічних дослідженнях. – К. : 2004 р., с. 24 – 32.