3.3. Forces of inertia and attraction-repulsion
V. I. Melnikov
As an example of application of the model proposed we consider some aspects of the behavior of the system consisting of a physical body with some mass (further – a mass) and a perfect vacuum surrounding this mass. The vacuum is considered as the equivalent object of interaction, since it, in accordance with condition 1, has the properties which differ from the properties of the mass placed into it.
In consequence of the apparent difference of mass and vacuum states, according to a condition 1, some hypothetical process of interaction appears between them. It is characterized by a particular flow moving between mass and vacuum (condition 6). At present, the activity of a perfect vacuum and the possibility that it enters interaction attract the attention of many physicists [7]. The vacuum is not a full void any more, and it represents a medium filled with infinite number of different virtual particles generating quantum fluctuations. According to condition 2 the criterion of the process existence is the change of experimentally discovered properties of the vacuum around of mass, for example, the appearance of the field intensity. Let us call conditionally this interaction as "mass" interaction.
According to conditions 2 and 14 the vacuum properties during the process of interaction will vary, it will cease to be vacuum in the own sense of this word, and the space around the mass will be filled by some products of interaction. According to condition 12 the level of interaction is proportional to the difference of body mass and vacuum (space with interaction products or interaction region), i.e. to the mass value. The intensity (density) of interaction in the isotropic space will decrease uniformly in all directions under the quadratic law with increasing distance from the mass because of the increase of the normal section of the flow in the isotropic space around the mass under the same quadratic law (note that the flow concept is widely used in the field theory as a tool of the description of the field parameters and their relations).
When there exists a flow component producing the appearance of mechanical forces, their resultant applied to the mass will be equal to zero (Fig. 6). In the case of inhomogeneous (anisotropic, asymmetric) interaction region around the mass, the mass will experience the action of the mechanical force.
It does not matter how the asymmetry is produced: at the expense of the asymmetry of the mass itself, putting in space other mass or other masses, the superposition of other kinds of interactions, irregular mass movement (at finite velocity of the interaction flow) or any different way.
In all the cases the difference of levels along the directions will be different, accordingly (the condition 12) the interaction intensity and unbalance of mechanical (and other) forces will be different. Thus, the gravity and inertial force can be interpreted as a particular case of the manifestation of asymmetric "mass" interaction. It is similarly possible to analyze the systems consisting of electric charges, magnetized bodies, and surrounding space.
The results of this analysis allow us to select the whole group of hypothetical processes presented at the bottom of Table 3. Thus, the functional similarity of the corresponding different values or their complexes arranged in a vertical direction is preserved. These are the processes of magnetic and electric interaction. The function of initiation will be performed by the parameters q1q2, J1J2, resistances ε0r2, μ0r2, changes Fэс, FM, quantitative accumulations Fэсt, FMt, powers KэсFэсq1q2, kMFMJ1J2, general produced works KэсFэсq1q2t, kMFMJ1J2t.
The model presented also allows one to obtain new qualitative and quantitative interpretation of the known empirical dependence of inertial force, mass and acceleration (the second Newton's law). In this case along with condition 12 and Table 3 we write:
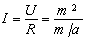
where I = Fин (inertial force) is the intensity; U = m2 is the level; m/a is the resistance R. (After substitutions we also obtain that Fин = a · m).
The corresponding new qualitative interpretation looks like this.
The mass moving with acceleration creates the asymmetry of environment (interaction region), the value of which is proportional to the value of mass m and acceleration a (Fig. 7). But the mass m simultaneously is the object placed to the same medium. Therefore the intensity I of the arisen interaction is proportional to m2. The complex m/a corresponds to the resistance R, since the same mass m prevents increasing of acceleration a, i.e. asymmetry of the interaction region. The acceleration a itself, in turn, increases the asymmetry of the interaction region, i.e. reduces the resistance R and increases the intensity I. In this case the mass m implements, as is seen, three functions.
The model of generalized process can be used to describe one-dimensional and two-dimensional systems, although they are studied much better than three-dimensional ones, both in theoretical and in applied aspects. Accordingly, the essential corrections in their sense are less probable. The model can also be used in the analysis of physical objects and processes of other kinds.
The nomenclature used in the description of the process of mass interaction with a physical vacuum is in direct correspondence with the nomenclature of the generally accepted apparatus of the field theory and some of its relations (see Table 3).
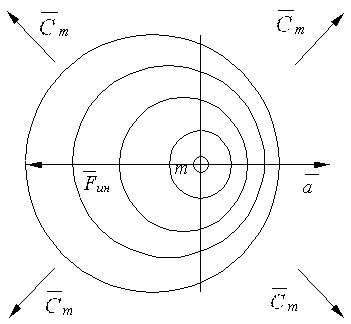
Fig. 7. Deformation of the interaction region at accelerated motion.
In particular, the following parallels are obvious:
Field – interaction region of mass with a physical vacuum (medium);
Intensity in the region point – specific intensity of a flow in the interaction region and, accordingly, specific mechanical force referred to a unit mass;
Potential in the field point – total energy of a flow with a unit mass located in the given point;
Potential difference – difference in total energy of the flow between two points of the interaction region;
Forces of gravitation and inertia – degree of asymmetry of the interaction region and, accordingly, asymmetry of interaction intensity along directions;
Mass – intensity parameter of “mass” interaction of a body with the surrounding physical vacuum (medium).
This correspondence confirms the legitimacy of the existence of the model considered, extends representation about the system "mass – vacuum", and also indicates the possibility of application of the field theory to investigate this system.
The dynamical model of a physical field is reflected in the correspondence stated above.
As an example of justification of the last conclusion we consider a hypothetical mechanism of inertial force origination at nonuniform motion of a mass in space. In accordance with the model, the inertia is intrinsic to the accelerated motion of any physical object which produces the asymmetry of the interaction region. The symmetry itself is the result of the accelerated motion of the object and the finiteness of the velocity of flow propagation of the corresponding kind of interaction (further wave, wave front).
For the case of "mass" interaction it is possible to obtain some quantitative relations. Figure 8 presents the scheme of accelerated rectilinear motion of the mass and the position of wave fronts of interaction at different instants. Thus, space is supposed to be uniform, and the mass is supposed to be point. From the point О at instant t, the mass “radiates” the wave of interaction propagating with a constant phase velocity cm in all directions relative to the points О and О1 (since Δt > 0, where Δt is the time of mass motion from the point О up to the point О1). The following notations are used: О is the point of "radiation" of interaction front at instant t = 0; О1 is the point of "radiation" of interaction front at instant (t + Δt); О2 is the position of mass at instant relative to which the value of inertial force is determined; А, А1, В, В1 are the positions of wave fronts of interaction at their motion along the line of displacement of mass from the point О to the point О2 at instant t1; t1 is the time of mass displacement from the point О to the point О2; (t1 – Δt) is the time of motion of the back edge of the wave front from the point О1 up to the points В and B1 in direct and return directions, respectively; Δt is the time of wave motion from the points B and B1 to the points A and A1, respectively;  and
and  are the mean vectors of the field intensity of "mass" interaction for intervals АВ and А1В1; a is the tangential acceleration of mass motion.
are the mean vectors of the field intensity of "mass" interaction for intervals АВ and А1В1; a is the tangential acceleration of mass motion.
We use the generally accepted description of the field theory with the corresponding parameters and notations.
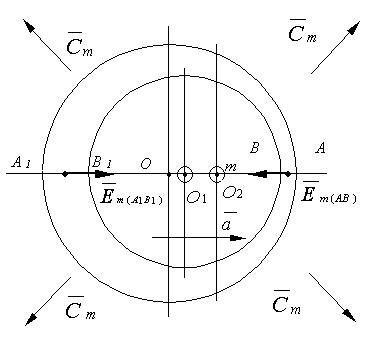
Fig. 8. Propagation of interaction flows at accelerated motion.
Let us consider the values of intensity vectors along the direction AA1 in the intervals АВ and А1В1. The field potential gradient in these intervals is assumed to be constant due to small Δt. The total field intensity along the direction AA1 is
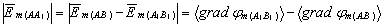 |
(18) |
where 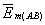 and
and 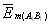 are the mean vectors of the field intensity in the intervals AB and А1В1, respectively;
are the mean vectors of the field intensity in the intervals AB and А1В1, respectively; 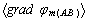 and
and 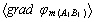 are the mean potential gradients of the field in the corresponding intervals; φm is the potential of the corresponding field point.
are the mean potential gradients of the field in the corresponding intervals; φm is the potential of the corresponding field point.
In turn,
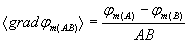 and
and 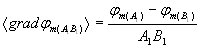 ,
,
where 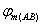 and
and 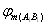 are the mean field potentials in the intervals АВ and А1В1.
are the mean field potentials in the intervals АВ and А1В1.
The potential values are determined from the following relationships:
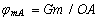 ;
; 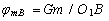 ;
;
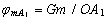 ;
; 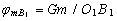 ,
,
where G is the gravitational constant; m is the mass value.
After the corresponding substitutions into equation (18), transformations and exception of the values of the maximum order of smallness, we obtain
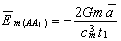
To determine the inertial force it is necessary to find the intensity vectors on the surface of the elementary generator of "radiation" (elementary mass), instead of the whole physical body with mass. Therefore, we can write:
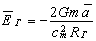
where Rr is the effective radius of the elementary generator of "radiation", Rr = cmt1.
The force acting from the side of field on the generator surface (inertial force) is
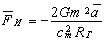
The sign minus at the right hand side of the equation means that the inertial force is directed to the side opposite to acceleration. Accordingly, the outer force accelerating the mass coincides in direction with acceleration, i.e. the outer force and the inertial force are equal in value and are opposite in direction.
The field intensity is usually determined in a point whose sizes can be neglected, the same is also valid for the radius of curvature of the corresponding isoline or isosurface of a field (Fig. 9). Such neglection is invalid for investigation of the self-field acting on the source, when its sizes (the sizes of elementary mass) are comparable to the effective radius of the field action. At the same time, there are no experimental data about the structure of the transition area between the source and the field. At the given stage of investigation this inconsistency is supposed to be eliminated by introducing a special coefficient of asymmetry taking into account the bending of the zone of the "internal" boundary of the field adjoint to the source, and by corresponding changing of directions of radial forces which act on the source from the side of the field. In this case, some total field intensity on the surface of the corresponding hemisphere of the source (Fig. 10) is defined more exactly. It is obvious that кa ~ 1 at considerable recession and кa ~ 0,5 at the maximum approach and minimum field deformation. At considerable field deformation by the accelerated motion we have 0,5 < кa < 1.
Therefore, the real total force of the field action on the mass (inertial force) is equal to
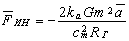
Thus, it is possible to state that the inertial force is the result of action on mass of a self-field deformed by its accelerated motion.
It is known from experiments that 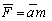 , therefore, after equating analytical and empirical inertial forces we can find (evaluate) the radius of "radiation" generator
, therefore, after equating analytical and empirical inertial forces we can find (evaluate) the radius of "radiation" generator
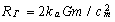
.
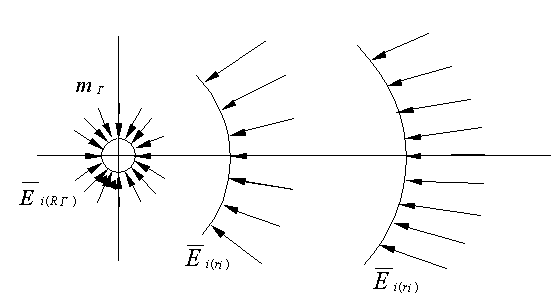
Fig. 9. Vectors of field intensity in isotropic field (without scale).
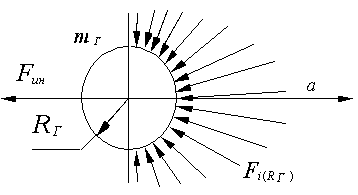
Fig. 10. Resultant forces in the source-field transition zone in a deformed field.
At the estimation of generator sizes for the best accuracy it is necessary to take the minimum mass of known masses of physical particles.
The expression obtained coincides in its form with the expression for the gravitational radius obtained for the first time by Leibnitz and used in the TGR [113], but its physical sense is completely other in this case.
Let us remark that the technique of investigation presented is valid for a source of any nature and also for definition of gravity (see below).
The results of numerical calculations of the values Rr for the "mass" and electromagnetic interaction (proton and electron) are presented in Table 4. It was supposed that сm = с, where с is the speed of light in vacuum and кa = 0,6. Note that the last measurements by Kopeikin and Flamont (2002) conducted with the help of radio emission of the quasar J0842+1835 passing through the gravitational Jovian lens confirmed that  [30].
[30].
Table 4. Estimated values of the sizes of generators of gravitational and electric radiation for electron and proton
| Object | Initial parameters | Radius of object, m | Rr, m | |||
| Charge, C | Mass, kg | Speed of front, m/s | Coefficients кa | |||
| Electron | 1,6·10-19 | 2,998·108 | 1/8,85·10-12 F/m | 2,82·10-15 | 2,4·10-25 | |
| 9,1·10-31 | сm | 6,67·10-11 m3/kg·s2 | -«- | 7,74·10-58 | ||
| Proton | 1,6·10-19 | 2,998·108 | 1/8,85·10-12 F/m | 0,7·10-15 | 2,4·10-25 | |
| 1,67·10-27 | сm | 6,67·10-11 m3/kg·s2 | -«- | 14,88·10-55 | ||
The analysis of the considered process of "mass" interaction and the results of calculations allow us to make the following conclusions:
1. The gravitational field and the inertial field are different manifestations of one process of the "mass" interaction.
2. The mass value is the parameter of "mass" interaction intensity.
3. The inertial force arising at accelerated mass motion is produced by the asymmetric self-field acting on it and deformed by accelerated mass motion.
4. The sizes of radiation generators of the fields considered are many orders of magnitudes smaller than the sizes of electron and proton. This points to complexity of their structure.
5. Due to small sizes of the generator of "mass" radiation and, accordingly, of radiation carriers (gravitons), their experimental detection in immediate prospects is improbable.
6. It is possible to change the inertial force by changing the parameters of interaction of mass with the surrounding space, for example, by imposing other fields on the interaction region (for example, fields of other nucleons of a nucleus – the mass defect effect) (see Sec. 3.7).
Essential assumptions adopted by consideration of the given example allow us to speak only about a rough quantitative evaluation of the values obtained, which can be corrected at more detailed investigations.
The asymmetry can be created with the help of the superposition of two and more interaction regions of the corresponding sources (sinks) (Fig. 11). In this case the vacuum region concluded between the sources will possess a state distinguished from the state of outer regions, as a result of simultaneous interaction with several sources. Due to that, at their back action on the source, their resultant will not be equal to zero and in the case of availability of the mechanical component in a flow, the mechanical force will be applied to the last source. The force direction will be determined by the kind and direction of flows of interaction, in particular, by the type of disturbing effect: by a source, sink, or their determined combination.
The above-presented considerations are valid not only for gravitational, electric or magnetic interaction and not only for three-dimensional space. Similar dynamics should be observed at other kinds of states and interactions.
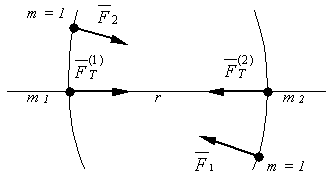
Fig. 11. Scheme of formation of gravity forces between two masses:
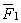 ,
, 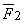 – are the forces applied to a unit mass from the side of masses m1 and m2;
– are the forces applied to a unit mass from the side of masses m1 and m2; 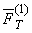 ,
, 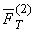 are the gravity forces acting on mass m1 from the side of mass m2 and on mass m2 from the side of mass m1, respectively.
are the gravity forces acting on mass m1 from the side of mass m2 and on mass m2 from the side of mass m1, respectively.
At present sufficiently perfect mathematical apparatus for the description of similar systems is available. In particular, the Laplace and Poisson linear partial differential equations are used for three-dimensional systems with distributed parameters.
For the case of a point object (the charge, mass, either other source or sink) in many important applications the solutions are convenient to find with the help of the influence function (Green function) in unbounded uniform space. It is equal to
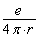 ,
,
where е is the source intensity; r is the distance from the point of influence to the source. These equations and their solutions, which are used in the field theory, (in particular, potential) are of important value in investigation of gravitational fields, magneto-, and electrostatics, diffusion, heat conduction, incompressible fluid, etc., and in this case for definition of the force value arising in asymmetric interaction region.
The gradient of total field influence in the point О2 (Fig. 11), i.e. the force applied to a unit of object state is
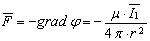 ,
,
where r = O1O2; μ is the coefficient taking into account the nature of interaction, properties of medium (interaction region) and selected system of measurement; 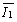 is the action intensity of the object О1 (charge, mass).
is the action intensity of the object О1 (charge, mass).
The total force (for example, gravitation) acting on object О2 with the intensity of action 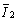 from the side of object О1 is
from the side of object О1 is
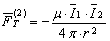 ,
,
or, similarly,
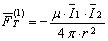 ,
,
where 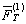 is the force acting on object О1 with the intensity
is the force acting on object О1 with the intensity  from the side of object О2 with intensity
from the side of object О2 with intensity 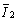 .
.
The experiment demonstrates that for the system mass – vacuum – mass
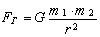 ,
,
where G is the gravitational constant; m1, m2 are the masses of the first and second objects.
From here we have
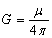 .
.
The similar expression is obtained, as is known, for the case of electrostatic charges or magnetized bodies.
At interpretation of object as a source of incompressible fluid the validity of the results presented is obvious because of a difference of total axial jet forces in the right and left-hand half-spaces arising because of increased drag to the outflow of fluid from the side of an adjacent source.
From the above-mentioned points it also follows that as the mechanism of action of the asymmetric medium on a sink or source is the same in all cases, the inertial forces and gravitation will arise at any kinds of interaction, under condition of availability of mechanical component in a flow.
The principle of equivalence of inertial and gravitational mass as different forms of manifestation of the same kind of mass interaction automatically follows from the similarity of this mechanism.
