3.5. Spatial velocity of objects
V. I. Melnikov
Displacement, velocity, and acceleration are the main parameters of the mechanical motion. Velocity may seem to be one of the best studied and simple quantities in physics, mathematics, and applied science.
The relationship of energy and velocity and its dependence on the physical nature of moving objects are much less comprehended points.
In the framework of our generalized notation, the velocity of motion is expressed in terms of the interaction intensity I, which is written as
 |
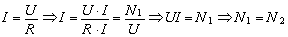(21) |
here U is the difference between the state levels; R is the resistance; N1 is the power withdrawn from the moving object; and N2 is the power spent on the change of the anti-object (path of travel).
The power N1 can be written as
N1 = N0 + Nвн,
where N0 is the internal energy spent by the moving object and Nвн is the external energy delivered to the object.
For the uniform mechanical straight-line motion under the action of the counter drag force (e.g., friction), we have
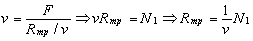
where v is the velocity of motion; F is the external force which maintains the motion; Rтр is the friction force; and N1 is the power delivered to the moving body.
Here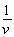 
is the coefficient of proportionality between the power N1 and the resistance force Rтр. The resistance force should decrease/increase with increasing/ decreasing v at constant N1, i.e., the ratio 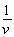is the index of the medium resistance to motion. To put emphasis on this point, let us introduce the designation
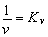
and write
Rтр = Kν;N1.
For the generalized process we can write similarly to relation (21) that
 |
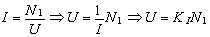(22) |
where KI is the coefficient of proportionality between the power delivered to the altered object and the level of the object’s resistance to these alterations.
Let us consider the question as to whether the form of this relationship is general for any particular case of motion, e.g., for the wave motion. The wave propagation being described with relation (29), the one-dimensional wave equation
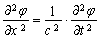
turns out to correspond to the expression for the generalized process. Indeed, let us rewrite the wave equation as a system of two equations:
 |
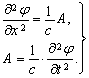(23) |
The partial derivative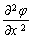 
is the specific gradient of the scalar potential of the continuous medium, and the derivative 
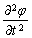is the specific rate of the temporal changes of this potential. In the case of acoustic waves, the derivative 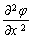can be interpreted as the specific tension, and the derivative 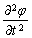can be interpreted as the specific rate of the temporal changes of this tension. The parameter A has dimensions of power, i.e., 
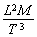, and the partial derivative 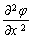has dimensions of force (Newton). So, the first equation can be rewritten as
,
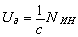where Ua is the magnitude of the deformation force and NИН is the power developing by the inertial forces.
The dimension of the scalar potential in the second equation is
,
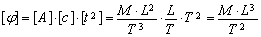hence we have
.
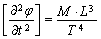By substituting these dimensional relations to Eq. (23), we obtain
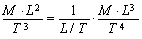
or
.
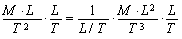After the cancellation we have
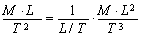
or
.
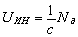Here UИН is the magnitude of the inertial force and Nd is the power developing by the deformation force.
Thus, the original wave equation for acoustic waves is transformed into two specific equations which describe the transformation of the inertial force into the deformation force and vice versa:
,
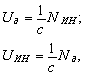Therefore, the wave equation for acoustic waves is the partial case of the generalized equation of mechanical motion (29). In both cases the parameter 1/c is the coefficient of proportionality between the power flux of the external action on the moving object (wave) and the object’s reaction on this action.
The wave equation for electromagnetic waves can also be transformed into the generalized equation of notation (29). To this end, one should consider the transverse oscillations described by the scalar φ and the vectors A, E, and H [116]. In the three-dimensional case, these quantities (the vectors are represented as the projections on the axes of the Cartesian coordinate system) satisfy the wave equation
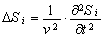, (i = 0…10),
where Δ is the Laplace operator,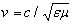 
is the phase speed of the electromagnetic wave, 
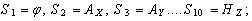and ε and μ are the relative permittivity and permeability of the medium.
This system can generally be transformed into a system of 20 equations, each of them being similar to generalized equation (22). Furthermore, any physical relations which contain the electrodynamic constant c can easily be transformed into the generalized equation of notation (22). For example, for the relation E = mc2 we have
.
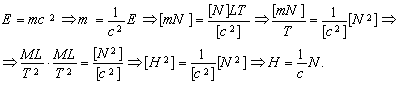Similarly we obtain
.
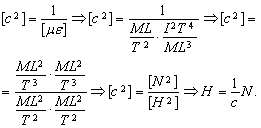There are many other similar examples of the transformations of the equations which include the parameter c.
Hence the electromagnetic wave propagation is the partial case of the generalized motion. So, it can be considered as an ordinary physical process with ordinary parameters.
Thus, generalized equation (29) is the basic equation for describing the spatial motion of the objects of any nature and for investigating any relevant physical process.