3.6. Redshift

V. I. Melnikov

Redshift was discovered by Slipher in 1914 from the spectra of several cosmic objects (extragalactic nebulae). In 1929 Hubble analyzed a larger body of data and found that redshift depends almost linearly on distance. Blueshift was discovered for nearby galaxies. Redshift is the fundamental concept in contemporary cosmological theories [15, 16, 17, 33, 34, 49, 94]. It is determined by the parameter

,

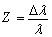where Δλ is the change of the wavelength of electromagnetic radiation and λ is the original wavelength.

The contemporary interpretation of the metagalactic redshift as the generalized Doppler effect is based on the supposition that Z is independent of λ. In the reference frame related to Metagalaxy, this effect is reduced to the longitudinal Doppler effect, which is caused by the frame deformation. Other explanations of the metagalactic redshift which referred to various hypothetic and real physical processes turned out to be insufficient. For example, the scattering of photons on the Dirac electron sea or the spontaneous light scattering by no means can lead to redshift, the emission of gravity waves by electromagnetic waves results in very small redshifts, and the scattering of photons on other particles produces lateral effects which are not observed in reality. Thus, the longitudinal Doppler effect is supposed to be the only known physical phenomenon which can be used to explain the properties of the metagalactic redshift.

The Doppler interpretation of redshift leads to the notion about the metagalactic expansion in which individual galaxies as well as galaxy clusters move away from one another, their relative distances increasing. This expansion, however, is not accompanied by the expansion of galaxies and cosmic bodies themselves.

Further development of the expansion theory led to the construction of numerous cosmological models of the universe. These models/theories are based on the theory of general relativity, the concepts of the inhomogeneous, isotropic, and anisotropic universe, the concept of the inhomogeneity/homogeneity of the space-time continuum, various assumptions about the mass distribution in the universe, and other prerequisites.

Such a variety of new theories owe their existence to the following problematic points [33, 34].

1. Multiplicity of models. First of all, for any cosmological constant the Einstein equations admit homogeneous isotropic models of different kinds which differ in parameter k (at cosmological constant 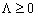) and in their temporal behavior. Secondly, the equations have a continuum of solutions for any such model. The multiplicity of models is quite natural when they are applied to bounded regions of the universe. However, the model of the universe as a whole should be unique, just like the universe itself (if such a model can be constructed at all).

2. Unexplained empirical relationship of metagalactic parameters with microphysical constants. The dimensionless ratios Q₁ = mc³ / e³H and Q₂ = m⁴c⁶ / e⁶ρ of the microphysical parameters composed of light speed c, elementary charge e, and electron mass m to the Hubble constant H and to the mean density of matter in the universe ρ differ little as to their orders of magnitude (which are about 10⁴⁰) at the present epoch. These ratios are also very close to the ratio Q₃ = e² / γ m m_p of the electrostatic force and the gravitational force acting between a proton and an electron (here m_p is the proton mass and γ is the gravitational constant). These two coincidences lead to other coincidences, e.g., the number of nucleons in a sphere of radius сН^-1, Q₄ = 4 π c³p / 3 m_p H², is close to Q₁², Q₂², Q₃². Note that the models with algebraic relationship between H and ρ retain only one independent coincidence. Such coincidences cannot apparently be explained solely in the framework of the gravitation theory. They probably refer only to some limiting values of metagalactic parameters. They may have only cosmogonic significance when the models are applied to bounded regions of the universe. However, they are of essentially cosmological significance in regard to the model of the universe as a whole.

3. Existence of singularities (“special sates”) at the beginning of expansion (except for the models of kinds A₂ and M₂ at Λ > 0) and at the end of expansion. Such singularities in solutions demarcate the time interval on which the theory is applicable or makes sense. This may be an indication of the insufficiency of the Einsteinian gravitation theory for very high densities (larger than nuclear densities). In reference to the universe as a whole, the singularities were interpreted as time boundaries (the beginning and the end of the existence of the universe). Such an interpretation was evidently used for theological deductions. In line with these speculations, it was supposed that the origin of chemical elements can be explained by the transition of the universe through some states close to the special ones. This point of view strengthened the notion of the expansion from a “special state”. At present the origin of elements is explained in broad outline in the theory of stellar evolution, with no regard to the special-state concept.

4. Time scale problem (the discrepancy between the expansion epoch duration T and cosmogonic estimates of object ages). According to the old scale of metagalactic distances which had been used before 1952, we had H₀^-1 = 1.8 10⁹ yr. This estimate is smaller than the estimated ages of the Earth’s crust and chemical elements, and this fact leads to contradiction at Λ <= 0, when T < H₀^-1. This contradiction was done away with by assuming that Λ > 0, inasmuch as old empirical estimates of q0 were much less accurate than the contemporary estimates. In this case, however, the expansion epoch duration was still inconsistent with the ages of galaxies and galaxy clusters estimated at 10¹² – 10¹³ yr. These estimates were obtained in 1920–1930 in the framework of statistical and mechanical approaches (the so-called long scale as opposed to the short scale with a length of 10⁹ – 10¹⁰ yr).

Later the long scale was abandoned almost completely in view of its inconsistence. At present we can speak about some discrepancies between the expansion epoch duration and the age of oldest stars and galaxies only within the bounds of the short scale.

5. Cosmogonic contradictions in the explanations of the origin of various cosmic objects under the present-day physical conditions. In view of these contradictions, it was originally supposed that cosmic objects were formed at past epochs, when physical conditions differed from those nowadays. Such suppositions referred to high-density states in models with singularities, to the stage of weakly accelerated expansion in the models of kinds A₂ and M₁ (Λ > 0), and to the epoch of everlasting contraction in the model of kind M₂ (Λ > 0). However, more recent studies showed that there are stars and galaxies of various ages and that their formation (from diffuse or dense matter) apparently continues at present. The contradictions in the explanations of the origin of stars and galaxies refer to cosmogony rather than to cosmology.

6. Deviations from homogeneity and isotropy in the distribution and motion of galaxies. They indicate that the applicability of the homogeneity and isotropy postulates is restricted to large, less investigated, scales.

These problematic points (except for the last one) played their part in the birth of new theories of the homogeneous and isotropic universe. The singularity problem, the time scale problems in their contemporary formulations, and the deviations from homogeneity and isotropy are of major significance in the development of the theory of the anisotropic inhomogeneous universe.

Einstein, de Sitter, Fridman, Robertson, Lemaître, Petrov, Eddington, Dirac, Jordan, Milne, Bond, Gold, Hoyle, Gamov, Alpher, Zel’dovich, Peebles, Guth, Linde, Alfvén, Sakharov, and others [15, 31, 33, 49, 82, 85, 94, 113, 115] attempted to eliminate the above-mentioned difficulties (as well as other ones), but the prerequisites of their models turned out to be incomplete or incorrect. Some models required essentially novel formulations of basic cosmological concepts, including the cosmology definition itself as well as the concept of the universe [34].

The theory of closed systems (TCS) and the model of the generalized physical process developed on the basis of the TSC (Sec. 3.2) can be used to introduce essentially new formulations of the well-known cosmological problems. The model of the generalized physical process (hereafter referred to as model) allows redshift to be interpreted as the result of some hypothetic process of wave energy dissipation, which is proportional to the distance travelled.

According to the model, electromagnetic wave propagation is an ordinary physical process described by a number of generalized parameters such as level, intensity, resistance, power, etc.

The generalized intensity of any process is written as

I = U / R

where I and U are the process intensity and level, and R is the resistance which is overcome by the process level (Sec. 3.2). The level U includes all active forces which maintain the process, and the resistance R comprises all the impeding factors. The intensity I characterizes the result of the counteraction between active and impeding factors.

In the case of spatial motion, the intensity has the meaning of the velocity of motion, the level characterizes the generalized governing force F₀, and R₀ is the specific generalized reaction force corresponding to the velocity v, namely,

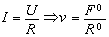(24)

In terms of the generalized power parameter, we have

(25)

where N₁⁰ is the generalized power transmitted by the generalized external force F⁰ to the moving object, and N₂⁰ is the generalized power consumed by the generalized reaction force R⁰v. The energy conservation law holds true when N₁⁰ = N₂⁰. It follows from (39) and (40) that v = ∞ at R⁰ = 0, F⁰ = const and v < ∞ at R⁰ > 0, F⁰ = const.

The action of an external force on a body with mass produces accelerated motion when there is no resistance R. On the other hand, the asymmetry of the region of the secondary interaction between this force and the surrounding vacuum is responsible for the generation of the inertial force directed opposite to the direction of motion (Secs. 3.2 and 3.3).

Similarly, any photon affects the state of the spatial points it propagates through. The regions which experience the action of the photon interact with the surrounding medium (the so-called secondary or lateral processes, see Sec. 1.2). So, the photon as the moving element of the alternating electromagnetic field interacts not only with the spatial points lying along the line of its motion but also (in view of the state difference) with the surrounding medium. This lateral interaction changes the photon state (in particular, energy). The amount of spent energy is proportional to the volume of the entire medium affected by the photon, i.e., to the path travelled. Therefore, electromagnetic waves lose their energy while they propagate. When there is no external energy source, the decrease of the photon energy E = ħω leads to the decrease of the oscillation frequency ( (at ħ = const).

For the visible spectrum of electromagnetic waves, the frequency drop corresponds to the shift of the spectrum to the “red” side. The mechanism of such changes in the electromagnetic wave frequency requires further investigation, but the proper definition of the problem is the necessary prerequisite for the problem solution. Surely, there are some questions as to the model applicability to the partial case of the photon propagation. Another plausible question refers to the reasons of the departure of one partial physical process from the laws of the generalized process synthesized from the variety of other partial process.

Thus, the most likely conclusion is that the electromagnetic wave changes its frequency due to energy losses while it overcomes the medium resistance. So, the model confirms Dirac’s hypothesis about the photon “ageing” proposed as early as in the 1930s. The photon energy dissipation was also considered in [33].

The dissipation effects proportional to distance covered in the course of motion should also be peculiar to other partial processes, e.g., to the gravity wave propagation. This viewpoint changes our understanding of the structure, processes, and history of the universe. In particular, the following implications are expected.

1. The absence of any photometric, gravitational, and radiometric paradoxes.

2. Resolution of the inconsistences in the time scale and in the concepts of the beginning and the end of the world.

3. No necessity in singularities.

4. A closer relationship of the cosmological constants H and ( with the microphysical constants c, e, and m_e. Note that the electron mass has the electric nature, according to the model.

5. The unified model of the universe adequate to the real universe can be constructed on the basis of clauses 1–3.

On the other hand, the blueshift observed for some nearby galaxies can be explained by the Doppler effect as a result of peculiar motions of these galaxies. It is remarkable that blueshifted are nearby galaxies. In the case of such small distances, the electromagnetic wave dissipation effect cannot surpass the blueshift effect.

Table 4 summarizes the existing hypotheses of the universe expansion as compared to the photon dissipation hypothesis. The hypothesis of the expanding universe poses much more problems than it solves. The photon dissipation hypothesis does not explain the dissipation mechanism, but it poses virtually no new problems. The interpretation of the cosmological redshift as the consequence of some hypothetic process of electromagnetic wave dissipation in the course of wave motion resolves a considerable number of existing contradictions and favours the construction of the unified model of the universe.

Table 5. Interpretations of the cosmological redshift

Empirical data and logical contradictions		Possible explanations
		Doppler effect in the expanding universe	Photon dissipation
1.	Gravitational redshift	–	+
2.	Stellar brightness fading	–	+
3.	Redshift for remote galaxies	+	+
4.		+	possible
5.	cz = H0r for nearby galaxies	+	possible
6.	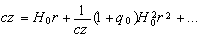for remote galaxies	–	possible
7.	Redshift anisotropy for nearby galaxies	–	possible
8.	The sizes of galaxies and cosmic bodies do not increase	–	not required
9.	Photometric paradox	+	+
10.	Gravitational paradox	+	+
11.	Radiometric paradox	+	+
12.	Dependence of redshift on stellar magnitude	–	+
13.	Empirical relationship of metagalactic and microphysical parameters	–	possible
14.	Contradictions between the probable age of cosmic objects and the age of the universe	–	possible
15.	Deviations in the distribution and motion of galaxies	–	not required
16.	Violation of conservation laws	–	not required
17.	Violation of relativity principles	–	not required
18.	Expansion cause	–	not required
19.	Beginning and end of the world	–	not required
20.	Existence of singularity	–	not required
21.	Multiplicity of models	–	not required
22.	Kinematic foundation of the world	–	not required
23.	One partial ordinary physical process lies in the foundation of the formation of the universe	–	not required

* minus sign: no explanation, plus sign: there exists some explanation