3.1.2. Entropy
V. I. Melnikov
In thermodynamics entropy is a function of state which characterizes the direction of behavior of spontaneous processes in a thermodynamic CS [33]. The existence of the entropy as a function of state is postulated by the second law of thermodynamics.
The difference of the system entropy in arbitrary states A and B is
,
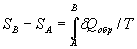where δQобр is the heat quantity transmitting to a system at an infinitesimal quasistatic change of its state; T is the absolute temperature at which heat is absorbed by a system.
The integral is taken at any reversible path connecting both states. In the case of isometric process ΔS = Qобр/T. For example, the entropy change at liquid vaporization is equal to the hidden heat of vaporization divided by the vaporization temperature.
For arbitrary reversible circular process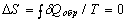 
. This equality is the necessary and sufficient condition for 
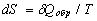to be a total differential and for the entropy to be a function of state. With δQ determined from the first law of thermodynamics, we have dS = (dU + pdV)/T, where U is the internal energy, p is the pressure, V is the volume. In this case the reversibility is guaranteed a priori.
The absolute value of entropy is determined by the third law of thermodynamics, according to which the entropy tends to zero at zero absolute temperature. It is some kind of entropy-temperature АCS.
In adiabatic CSs the entropy remains to be constant in the case of reversible processes (i.e. in thermal АCSs), and it increases in the case of irreversible processes. In all real processes, entropy increases due to disclosure of all real CSs (the law of entropy increasing). The state in which the entropy of an adiabatic system is maximum is by definition the state of undamped thermodynamic equilibrium, in which further macroscopic changes do not occur until external conditions change.
The concept of "entropy" was introduced by Clausius (1865) for the elimination of the inconsistency between the energy conservation law and the results of experimental investigations of reversible thermodynamic processes in CSs. In particular, it was proved that the total energy in a system decreases in the course of the cyclical transformation of the thermal energy into the mechanical energy and backwards. Entropy, according to the conception of its "creators", should have explained quantitatively the energy deficit cause. The known forms of notation (differential and integral) as well as the development and extension of this concept extended the area of its application to statistical physics, cosmology, information theory, and other sciences. The continuous growth of its influence on the development of physics and other sciences indicates the existence of deep connections of this phenomenological concept with the fundamental laws of the universe.
Now the entropy concept is connected with the concept of structure, chaos, ordering, monotonicity, self-organization, etc. And, much more likely, the extension of the content of this concept has not finished yet.
The ТCS allows us to deepen our notion about the "entropy" concept, to extend the limits of its applicability, and to predict its new properties and relationship with other fundamental concepts.
1. In the context of the ТCS, any real closed system is a CCS which is in the state of very weak interaction with the surrounding universe. Accordingly, the total state of CCS parts should thereby vary, and we can write
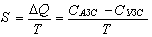
where ΔQ is the energy loss in transformations; СACS, СCCS are the ACS and CCS states, respectively.
2. According to Sec. 1.2, the separating zone is characterized by a function of deceleration (resistance). Therefore, energy losses are inevitable when heat is transformed into mechanical action and backwards and when interaction flow propagates through this zone. With allowance for clause 1, it is impossible to satisfy perfectly the conditions of adiabatic process. The energy of the reversible process changes at the expense of the entropy supplied by the surrounding medium.
3. The "state" concept is a complex concept. It embraces the measured and structured terms (matter, energy) as well as all other possible sources of action, including phenomenological (nonstructural) sources. So, the "state"concept as a whole is a phenomenological concept as well.
4. The generality of the "state" concept implies any correlations of its parts, including the availability of any component in pure form at the absence of other components. Therefore, the ТCS relations are all valid for the state which consists only of entropy.
5. In particular, it is possible to admit that the approach of levels of interacting objects (Sec. 1.2), i.e. the elimination of differences between them for the entropic case results in the destruction of structure and in the increase of chaos. In other words it represents the law of entropy increase.
6. The existence of the conservation law for the entropy in АСS is also possible as a particular case of the law of state conservation. Hence, the thermal death of the universe is impossible.
7. A "smooth" transition of the "entropy" concept to the "state" concept is possible as well, and the limits of its application can thereby be extended.
Thus, the consideration of the "entropy" concept in the ТCS context favors the extension of our notion about it, its properties, and the limits of its application.
It is quite apparent that the speculations presented here are only tentative, and the problem requires further investigation.